UNIT 1: INTRODUCTION TO AC SYSTEM

INDEX
| UNIT 1 : INTRODUCTION TO ALTERNATING CURRENT AND VOLTAGE |
| 1.1 AC System 1.2 The Sine Wave 1.3 Sinusoidal Voltage Source 1.3.1 An AC Generator 1.4 Voltage and Current Values of Sine Waves 1.4.1 Instantaneous Value 1.4.2 Peak Value 1.4.3 Peak-peak Value 1.4.4 RMS Value 1.4.5 Average Value 1.5 Angular Measurement of Sine Waves 1.5.1 Angular Measurement 1.5.2 Phase of Sine Wave 1.6 The Sine Wave Formula 1.6.1 Expression for Phase-Shifted Sine Wave 1.7 Introduction to Phasors 1.8 Analysis of AC Circuits 1.8.1 Ohm’s Law 1.8.2 Kirchhoff’s Law 1.9 Superimposed DC and AC Voltages 1.10 Summary 1.11 Self-Assessments |
Learning Objective:
The objective of this unit is to:
- Identify a sinusoidal waveform and measure its characteristics
- Describe how sine waves are generated
- Determine the various voltage and current values of sine wave
- Describe the angular relationships of sine wave
- Mathematically analyze a sinusoidal waveform
- Use a phasor to represent a sine wave
- Apply the basic circuit laws such as Ohm’s law and Kirchoff’s law in analyzing the basic ac circuits
- Determine total voltages that have both ac and dc components
Learning Outcome:
At the end of lesson student should be able:
- Familiarize with the characteristics of a sinusoidal waveform including its general format, average value, and effective value.
- Differentiate the expressions in time-domain and phasor-domain
- Determine the phase relationship between two sinusoidal waveforms of the same frequency.
- Calculate simple ac circuits using basic circuit laws
1.1 AC SYSTEM
An alternating electrical signal is a voltage or current waveform that changes consistently with time. In other words, it changes instantaneously with time. Both current and voltage have magnitude as well as positive and negative polarity.
An alternating voltage is the one that changes polarity at certain rate, v(t) = f(t), and also an alternating current is the one that changes direction at certain rate, i(t) = f(t). The sinusoidal waveform is most common and fundamental type compare to other types of repetitive waveform. The sine wave is a periodic type of waveform that repeats at fixed intervals.
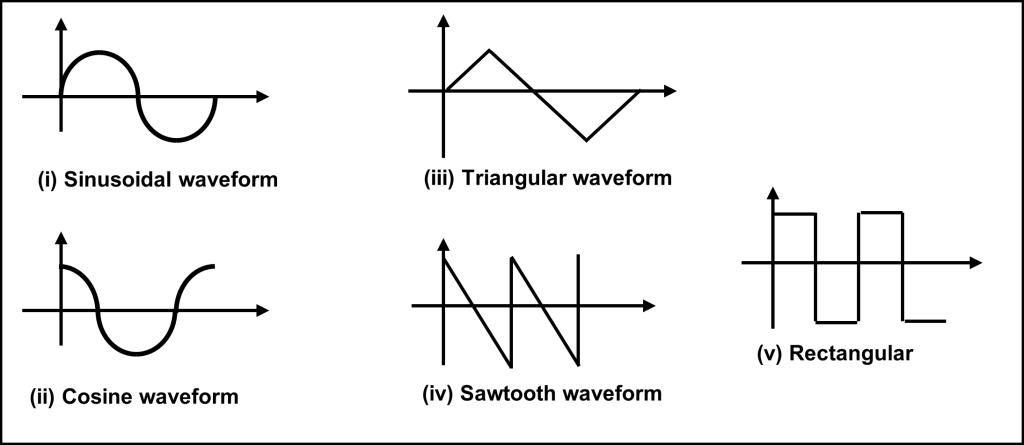
Special emphasis is given to sinusoidal waveform because of its fundamental importance in an ac circuit. There are various types of waveforms in an ac circuit (refer Figure 1.1) such as:
(i) Sinusoidal waveform
(ii) Cosine waveform
(iii) Triangular waveform
(iv) Sawtooth waveform
(iv) Rectangular waveform
An alternating waveform can be categorized into four main characteristics:
(i) Symmetry
(ii) Non-symmetry
(iii) Periodic
(iv) Non-periodic
Figure 1.2, 1.3, 1.4 and 1.5 below show the symmetry, non-symmetry, periodic and non-periodic waveform.
1.2 THE SINE WAVE
The sinusoidal waveform or sine wave is the fundamental type of alternating current (ac) and alternating voltage. It is also referred to as a sinusoidal wave or simply, sinusoid.
Sinusoidal voltages are produced by two types of sources: rotating electrical machines (ac generators) or electronic oscillator circuits. Figure 1.6 shows the symbol used to represent source of sinusoidal voltage.
Figure 1.7 is a graph showing the general shape of sine wave, which can be either an alternating voltage or an alternating current. The magnitude for voltage (or current) is displayed oh the vertical axis and time (t) is displayed on the horizontal axis. Starting at zero, the voltage (or current) increases to a positive maximum (peak), returns to zero, and then increases to a negative maximum (peak) before returning again to zero, thus completing one full cycle.

Figure 1.6: Symbol for sinusoidal voltage source
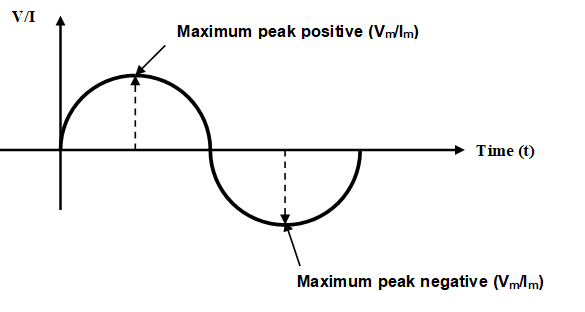
Figure 1.7: Graph of one cycle of a sine wave
Period of Sine Wave, T
A sine wave varies with time (t) in a definable manner.
Period can be defined as the time required for a sine wave to make a complete one full cycle.
The symbol for period is T and the unit is measured in second. Figure 1.8 (a) illustrates the period of a sine wave and Figure 1.8 (b) shows the repetition of sine wave at an equal time interval.
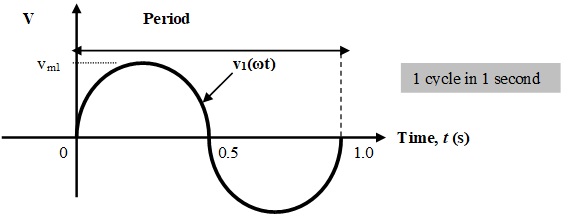
Figure 1.8 (a)
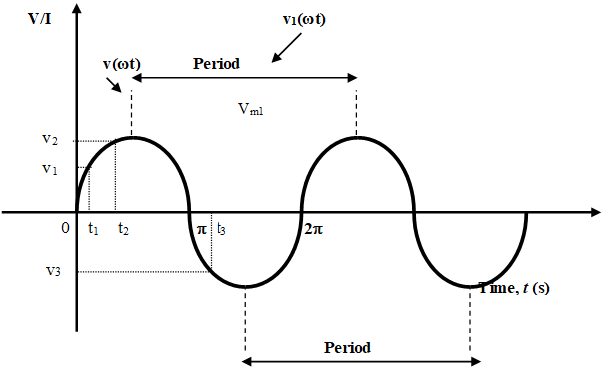
Figure 1.8 (b)
Notes:
A period for one cycle of a sine wave is measured from zero until 2π or from maximum positive peak on the first cycle to the second maximum positive peak on the second cycle. This is illustrated in Figure 1.8 (b).
Example 1.1 :
What is the period of the sine wave in Figure 1.9
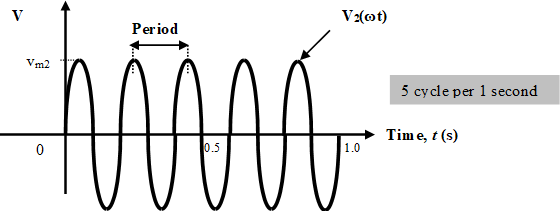
Figure 1.9
Solution :
5 cycles in 1 sec
1 cycle = 1/5 = 0.2 sec
Since 1 cycle = T = 0.2 sec
Related Problem:
What is the period if the sine wave goes through eight cycles in 20 seconds?
Example 1.2 :
Measurements are as indicated in Figure 1.10, where two cycles of sine wave are shown. If a first positive peak occurs at 2ms and the next positive peak occurs at 10ms, what is the period?
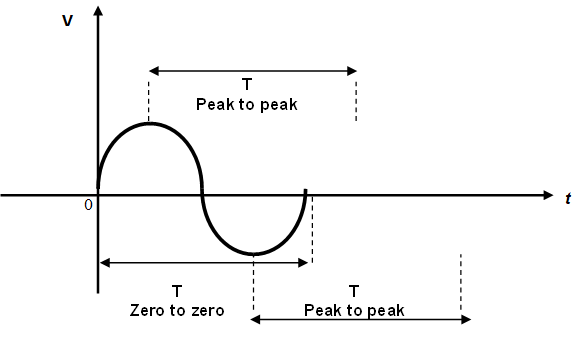
Figure 1.10
Solution :
Period, T = One cycle = 10ms – 2ms = 8ms
Frequency of a Sine Wave, f
Frequency (f) is the number of cycles that a sine wave completes in one second.
The symbol for frequency is f and the unit is measured in hertz (Hz) or cycle per second.
The more cycles completed in one cycle, the higher is the frequency. Figure 1.11 shows two sine wave, where in (a) completes one cycle in one second whereas in (b) completes five cycles in one second. Therefore, the sine wave in (b) has five times the frequency of the one in (a)
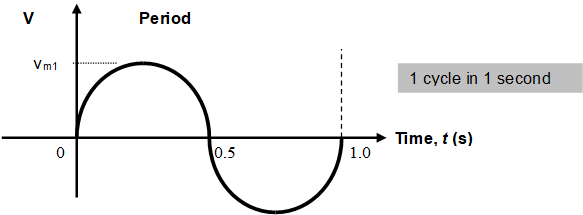
Figure 1.11 (a)
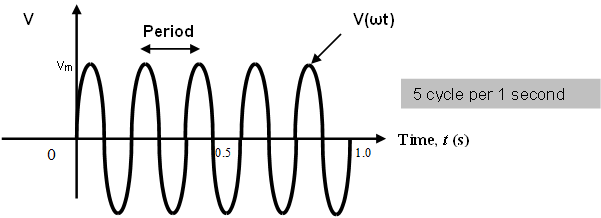
Figure 1.11(b)
Relationship of Frequency and Period
The formulas for the relationship between frequency (f) and period (T) are as follows:
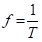
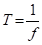
There is a reciprocal relationship between f and T.
Example 1.3 :
Which sine wave in Figure 1.12 below has a higher frequency? Determine the frequency and the period f both waveforms.

Figure 1.12
Solution :
Waveform (b) has higher frequency compare to waveform (a).
For waveform (a):
There are 2 cycles in 1 second. Therefore, one complete cycle the Period, (T) = ½ sec = 0.5 sec and the frequency, (f) = 1/T = 1/0.5 = 2 Hz.
For waveform (b):
There are 6 cycles in 1 second. Therefore, one complete cycle the Period, (T) = 1/6 sec = 0.167 sec and the frequency, (f) = 1/T = 1/0.167 = 6 Hz.
Related Problem:
If the time between the negative peaks of a given sine wave is 50 µs, what is the frequency?
Example 1.4 :
The frequency of a sine wave is 60 Hz. What is the period?
Solution :
Use equation 1.2
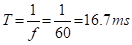
Related Problem :
A certain sine wave goes through four cycles in 20ms, what is the frequency?
1.3 SINUSOIDAL VOLTAGE SOURCE
1.3.1 AN AC GENERATOR
In the simplest form of generator the conductor is an open coil of wire rotating between the poles of a permanent magnet. During a single rotation, one side of the coil passes through the magnetic field first in one direction and then in the other, so that the induced current is alternating current (AC), moving first in one direction, then in the other. Each end of the coil is attached to a separate metal slip ring that rotates with the coil. Brushes that rest on the slip rings are attached to the external circuit. Thus the current flows from the coil to the slip rings, then through the brushes to the external circuit as shown in
Figure 1.13.
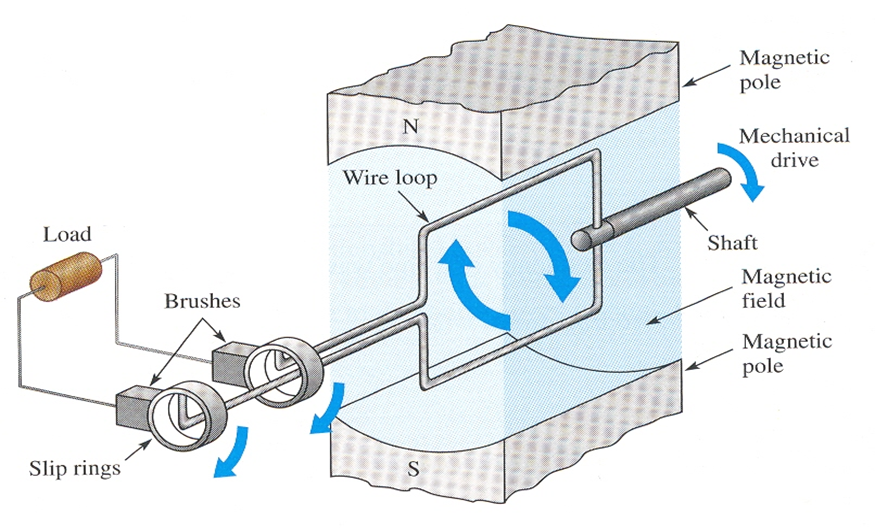
Figure 1.13: A simplified ac generator
To begin with, refer to Figure 1.14 (a) shows the wire loop rotating through the first quarter of a revolution. Starting at the horizontal position, where the induced voltage is zero, to a vertical position, where the induced voltage is at maximum. At the horizontal position, it can be seen that the loop is moving parallel with the flux lines, that exist between the north (N) and south (S) poles of the magnet. Thus, no flux lines are being cut, therefore no voltage being induced which is zero voltage. As the wire loop rotates through the first quarter-cycle, it cuts through the flux lines at an increasing rate until it is moving perpendicular to the flux lines at the vertical position and cutting through at a maximum rate. This is shown on the display in Figure 1.14 (a), at this point of rotation it produces the first quarter of the sine wave cycle as the voltage increase from zero to its positive maximum.
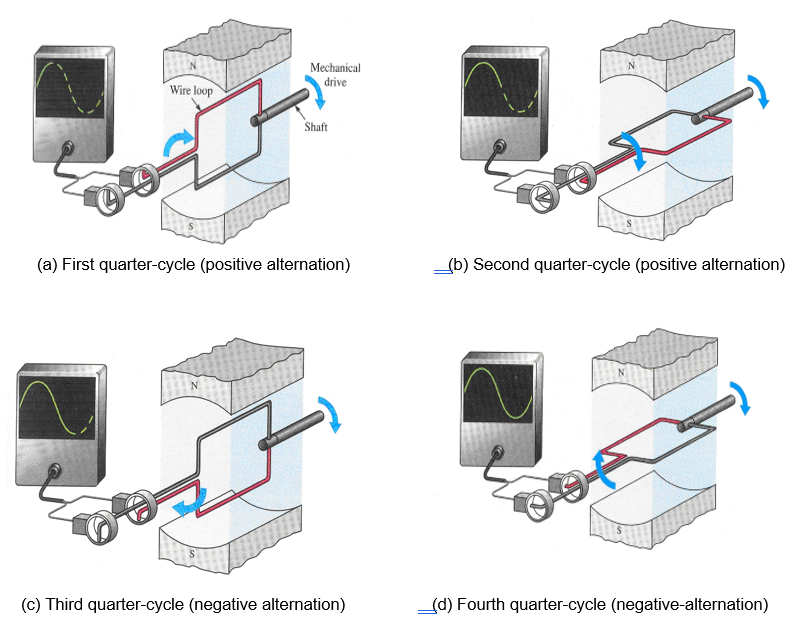
Figure 1.14: One revolution of the wire loop generates one cycle of the sinusoidal voltage.
Figure 1.14 (b) shows the loop completing the first half of a revolution. This part of rotation indicates that the voltage decreases from its positive maximum back to zero as the rate at which the loop cuts the flux lines also decreases.
During the second half of the rotation, as illustrated in Figure 1.14 (c) and 1.14 (d), the wire loop is cutting through the magnetic field in the opposite direction, so the induced voltage has a polarity opposite to that produced during the first half of the rotation. After one complete rotation of the loop, one full cycle of sinusoidal voltage has been induced. As the wire loop continues to rotate, repetitive cycles of sine wave are generated.
1.4 VOLTAGE AND CURRENT VALUES OF SINE WAVES
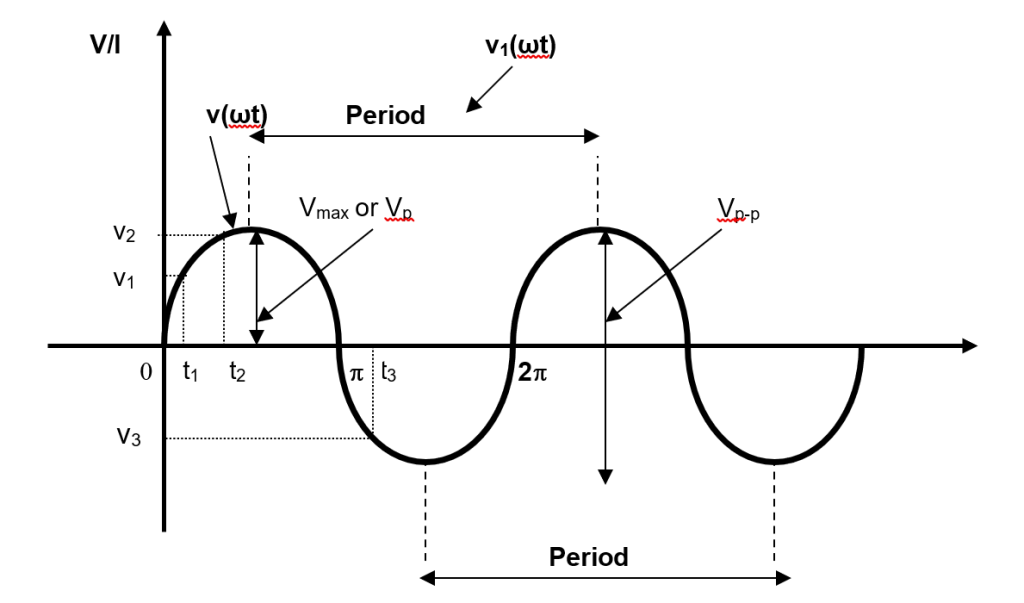
Figure 1.15
1.4.1 INSTANTANEOUS VALUE
Figure 1.15 illustrates that at any point in time on a sine wave, the voltage (or current) has an instantaneous value. This instantaneous value is different at different points along the curve for example at t1, t2and t3the instantaneous values of voltage are v1, v2 and v3 respectively. Instantaneous value of voltage and current are symbolized by lowercase v and i, respectively.
1.4.2 PEAK VALUE
The peak value of a sine wave is the value of voltage (or current) at the positive or negative maximum peak with respect to zero. This is illustrated I Figure 1.15, where for a given sine wave, the peak value is constant in magnitude and is represented by Vmax or Vp.
1.4.3 PEAK-TO-PEAK VALUE
The peak-to-peak value of a sine wave, as shown in Figure 1.15, is the voltage or current from positive peak to negative peak. It is always twice the peak value as expressed in equation 1.3 and equation 1.4. Peak-to-peak voltage or current values are represented by Vp-por Ip-p.
Vp-p = 2Vp Equation 1.3
Ip-p= 2Ip Equation 1.4
Example 1.5 :
For the sinusoidal waveform in Figure 1.16 below:
(a) What is the peak value?
(b) What is the instantaneous value at 0.1s?
(c) What is the peak to peak value of the waveform?
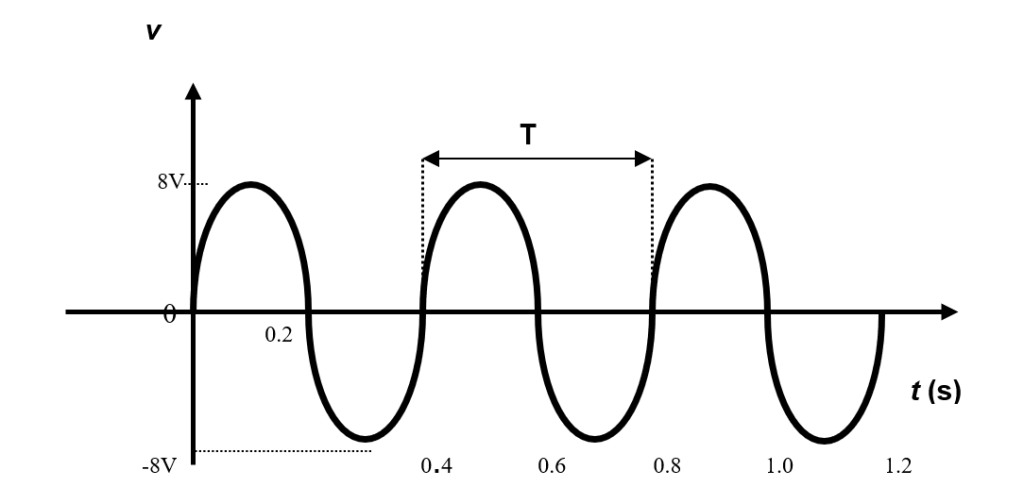
Figure 1.16
Solution :
(a) Vp = 8 Volt
(b) v(0.1) = Vp = 8 Volt
(c) Vp-p = 16 Volt
Related problem :
Refer to Figure 1.16
- What is the period of the waveform?
- What is the frequency of the waveform?
- How many cycles are shown?
1.4.4 RMS VALUE
RMS means root mean square. The rms value also referred to as the effective value of a sinusoidal voltage that measured the heating effect of the sine wave. For example, when a resistor is connected across an ac voltage source, a certain amount of heat is generated by power in the resistor.
The rms value of sinusoidal voltage is equal to the dc voltage that produces the same amount of heat in a resistance as does the sinusoidal voltage.
The peak value of a sine wave can be converted to the corresponding rms value using the following relationship, either voltage or current:
Vrms = 0.707 Vp Equation 1.5
Irms = 0.707 Ip Equation 1.6
Equation 1.5 and 1.6 are applicable only for sinusoidal waveform.
The equation below is applied to obtain the rms value for other waveforms.
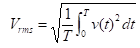
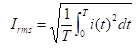
By using equation 1.5 and equation 1.6, the peak and peak-to-peak values can be determined respectively.
Vp @ Ip = 1.414 Vrsm @ Irms Equation 1.9
Vp-p @ Ip-p = 2.828 Vrms @ Irms Equation 1.10
Example 1.6 :
Calculate the effective or rms value for the current waveform in Figure 1.17 below.
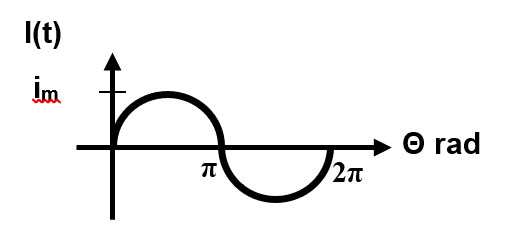
Figure 1.17
Solution :
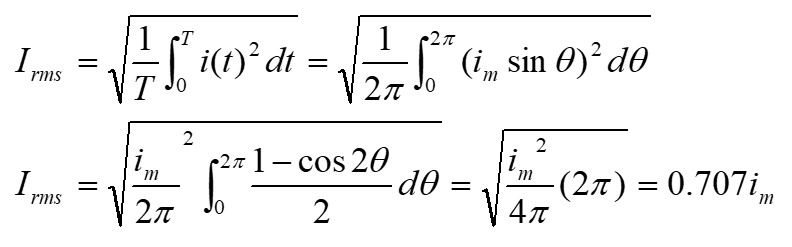
For a pure sine waveform, the relation between effective or rms value and peak value is given by:
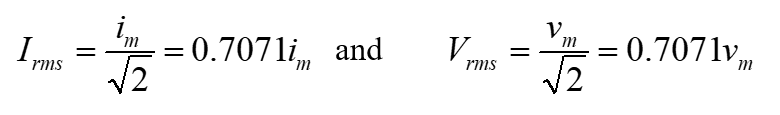
1.4.5 AVERAGE VALUE
The average value of a sine wave taken over one complete cycle is always zero because the positive value offset the negative value. So the average value of a sine wave is taken as the total area under the half-cycle curve divided by the distance in radians of the curve along the horizontal axis.
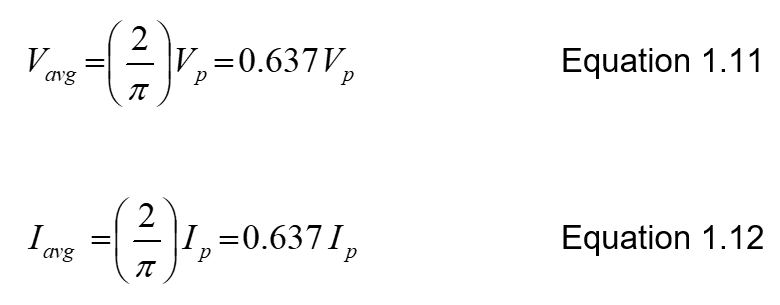
Equation 1.11 and 1.12 are applicable only for sinusoidal waveform.
The equation below is applied to obtain the average value for other waveforms.

Example 1.7 :
Refer Figure 1.18, find the average value for the sinusoidal waveform.
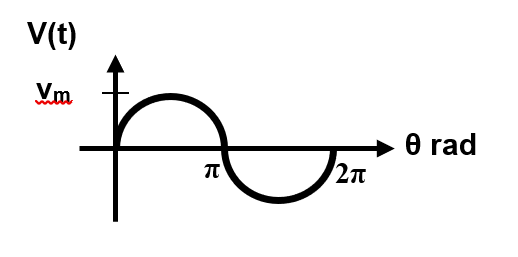
Figure 1.18
Solution :
Since sinusoidal wave is a symmetrical waveform, the value of T is taken for half-cycle only. Therefore, T = ½ cycle = π rad/s.
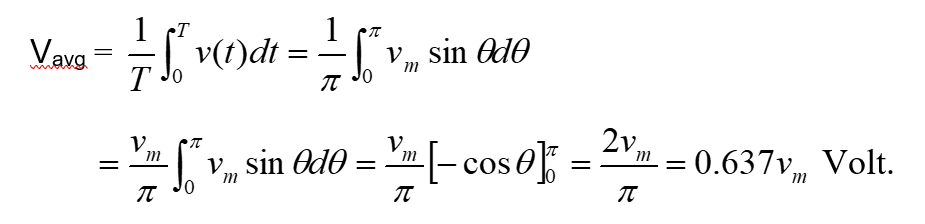
Therefore for a pure sine wave, the relation between average value and peak value can be summarized as:
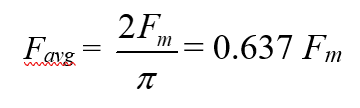
1.5 ANGULAR MEASUREMENT OF SINE WAVES
1.5.1 ANGULAR MEASUREMENT
A degree is an angular measurement corresponding to 1/360 of a circle or a complete revolution. A radian is the angular measurement along the circumference of a circle which is the radius of the circle. Figure 1.19 shows an angular measurement relationship of radian (rad) to degree (°) where one radian is equivalent to 57.3° and π is equal to 3.14. Table 1.0 and 2.0
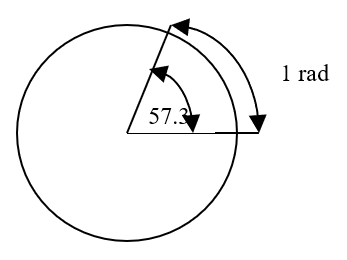
Figure 1.19: Angular measurement showing relationship of radians (rad) to degrees (°)
Table 1.0: Conversion from degrees to radians
| Degree | Radian |
| 90° | (π/180°) x (90°)= π/2 radian |
| 60° | (π/180°) x (60°)= π/3 radian |
| 30° | (π/180°) x (30°)= π/6 radian |
Table 2.0: Conversion from radian to degrees
| Radian | Degree |
| π/3 | (180°/π) x (π/3) = 60° |
| π | (180°/π) x (π) = 180° |
| 3π/2 | (180°/π) x (3π/2) = 270° |
Radian/Degree Conversion
Degrees can be converted to radians
Radian = (π rad/180°) x (degree) Equation 1.15
Similarly, radian can be converted to degree
Degree = (180°/π rad) x (radian) Equation 1.16
The velocity with which the radius vector rotates about the center is called angular velocity, and can be determined from the following equation:
The symbol used for angular velocity is the lowercase Greek letter omega (ω) and measured in radian/sec.
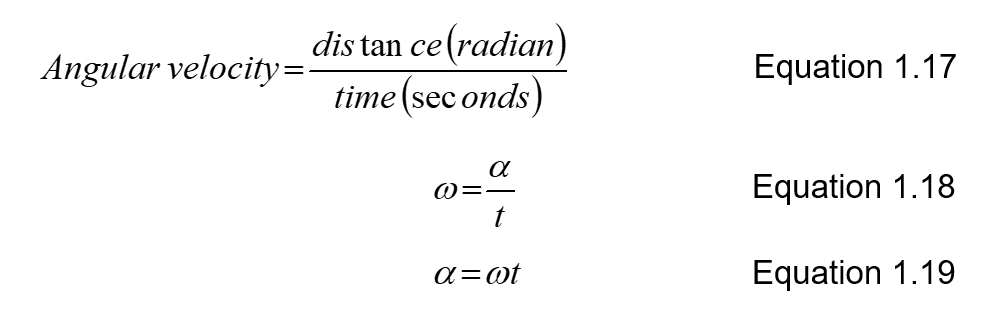
Example 1.8 :
(a) Convert 60° to radians (b) Convert π/6 rad to degrees
Solution :
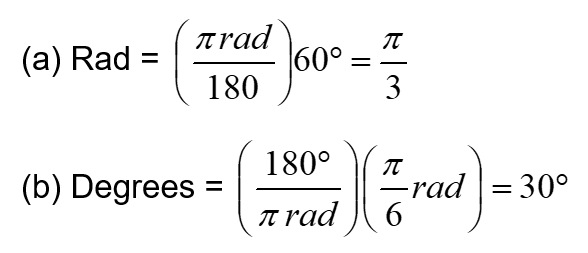
Related problem :
(a) Convert 15° to radians (b) Convert 5π/8 rad to degrees
1.5.2 PHASE OF SINE WAVE
The phase of a sine wave is an angular measurement that specifies the position of sine wave relative to a reference. Figure 1.20 shows one cycle of a sine wave to be used as the reference. Note that the first positive-going crossing of the horizontal axis (zero crossing) is at 0°(0 rad), and the positive peak at 90°(π/2 rad). The negative-going zero crossing is at 180° ( π rad), and the negative peak is at 270° (3π/2 rad). The cycle is completed at 360° (2π rad).
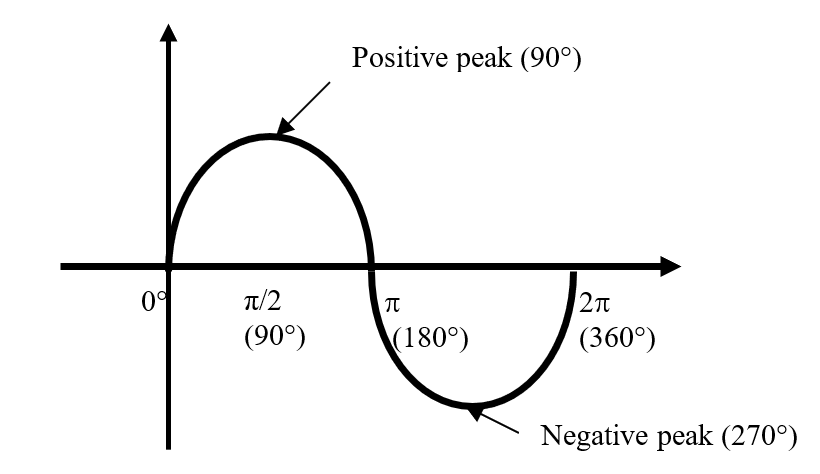
Figure 1.20: Phase reference
Figure 1.21 below illustrate phase shift of a sine wave. In Figure 1.21 (a), sine wave B is shifted to the right by 90° with respect to sine wave A. Thus, there is a phase angle of 90° between sine wave A and sine wave B. In terms of time, the positive peak of sine wave B occurs later than the positive peak sine wave A because time increases to the right along the horizontal axis. In this case, sine wave B is said to lag sine wave A by 90° or in other word, sine wave A leads sine wave B by 90°. In Figure 1.21 (b), sine wave B is shifted to the left by 90° with respect to sine wave A. In this case, the positive peak of sine wave B occurs earlier than positive peak sine wave A; therefore, sine wave B is said to leads sine wave A by 90°.
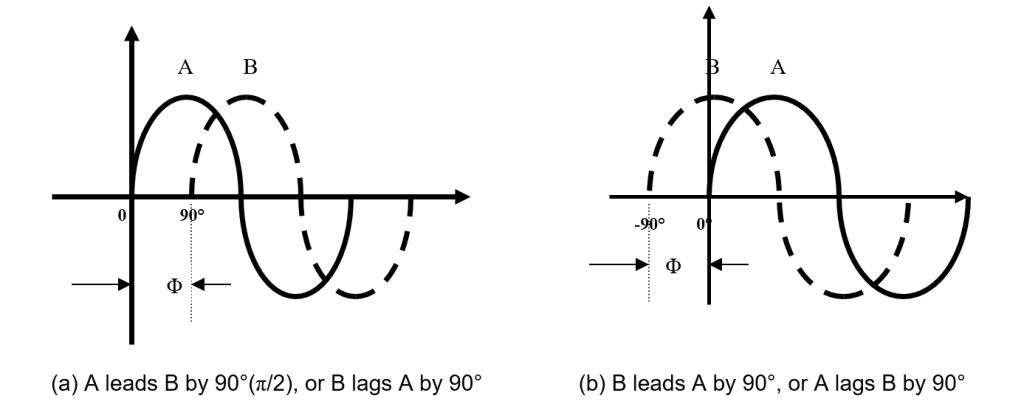
Figure 1.21: Illustration of phase shift
Example 1.9 :
What is the phase angle between the two sine wave in Figure 1.22.
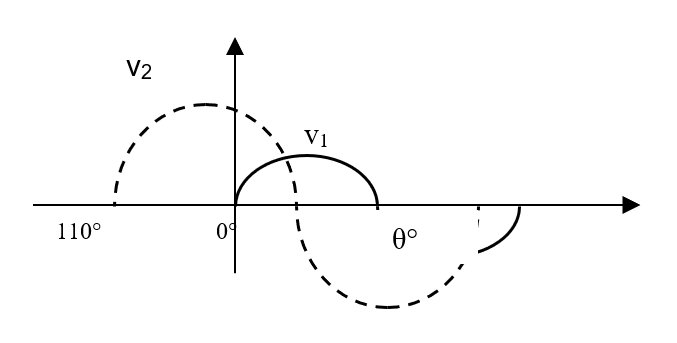
Figure 1.22
Solution :
Sine wave v2 is shifted to the left by 110° with respect to sine wave v1, where the positive peak of sine wave v2 occurs earlier than positive peak sine wave v1. Thus, sine wave v2 is said to leads sine wave v1 by 110°.
1.6 THE SINE WAVE FORMULA
The basic mathematical format for the sinusoidal waveform is
y = Am sin θ or Am sin ωt Equation 1.20
Where Am is the peak value of the waveform and θ is the unit of measure for the horizontal axis, as shown in Figure 1.23
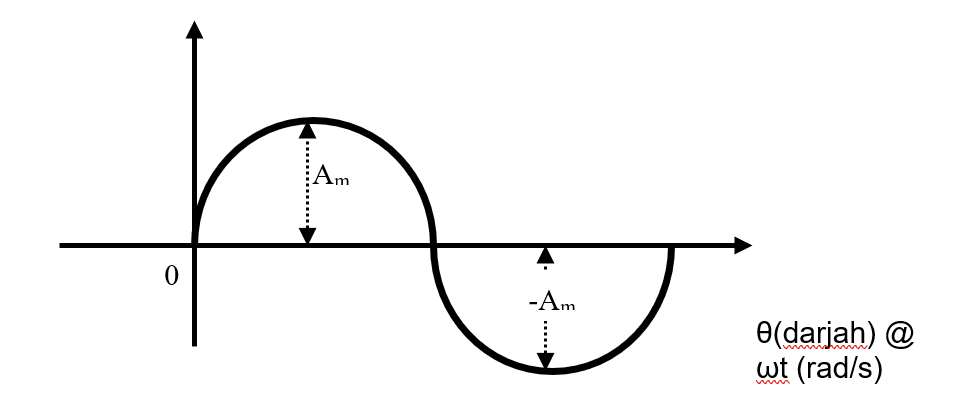
Figure 1.23: Basic sinusoidal function
For electrical quantities such as current and voltage, the general format is
i(t) = Im sin ωt = Im sin θ Equation 1.21
v(t) = Vm sin ωt = Vm sin θ Equation1.22
Where
Im and Vm is the maximum value or amplitude of the current and voltage.
1.6.1 EXPRESSIONS FOR PHASE-SHIFTED SINE WAVES
When a sine wave is shifted to the right of the reference (lagging) by a certain angle, Φ (Greek letter phi), as illustrated in Figure 1.21 (a) where the reference is the vertical axis, the general expression is
y = A sin (θ – Φ) Equation 1.23
where y represents instantaneous voltage or current, and A represents the peak or maximum value. When a sine wave is shifted to the left of the reference (leading) by a certain angle, Φ, as illustrated in Figure 1.21 (b), the general expression is
y = A sin (θ + Φ) Equation 1.24
Example 1.10 :
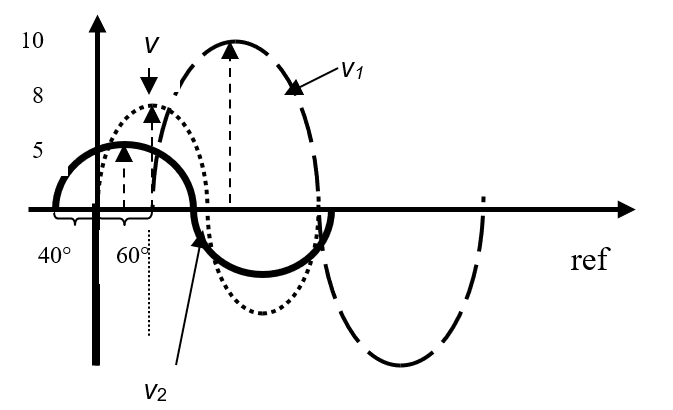
Figure 1.24
Refer to Figure 1.24, determine the instantaneous expression for v, v1 and v2.
Solution :
v(t) = 8 sin θ
v1(t) = 10 sin (θ – 60°)
v2(t) = 5 sin (θ + 40°)
1.7 INTRODUCTION TO PHASORS
Sinusoids are easily expressed in terms of phasors, which are more convenient to work with than sine and cosine functions.
A phasor is a complex number that represents the amplitude and phase of sinusoidal.
Phasors provide a simple means of analyzing linear circuits excited by sinusoidal sources; solution of such circuits would be intractable otherwise. Before completely define phasors and apply to circuit analysis, there is a need to familiarize with complex numbers.
A complex number z can be written in rectangular form as
z = x + j y
where
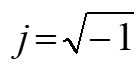
x is the real part of z; y is the imaginary part of z.
The complex number can also be written in polar or exponential form as
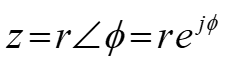
Where
r is the magnitude of z, and Φ is the phase of z.
In an ac circuit the phasor is represent by a straight line where the magnitude in rms value and phase angle, Φ in degrees (°) and both are measured from the vertical axis. For example, a sinusoidal waveform is given by an equation, v(t) = Vm sin (ωt + Φ°) Volt.
In phasor diagram representation, the voltage in time domain v(t) has to be converted phasor domain,
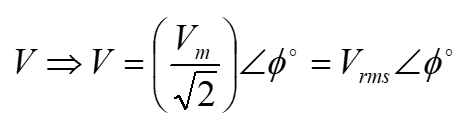
Volt, refer Figure 1.25 below.
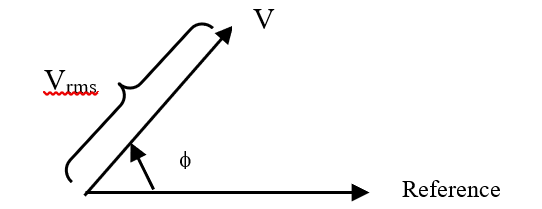
Figure 1.25: Voltage phasor representation
Table 3.0 below shows the sinusoid phasor transformation whereas Figure 1.26 shows an example of phasors diagram representation of an ac voltage and current.
Table 3.0: Sinusoid-phasor transformation


Figure 1.26: Graphical phasors representation of an ac voltage and current.
From Figure 1.26, it can be concluded that:
- I leads V by an angle θ° or V lags I by an angle θ°.
- V leads V1 by an angle Φ° or V1 lags V by an angle Φ°.
- I leads V1 by an angle (θ°+Φ°) or V1 lags I by an angle (θ°+Φ°).
Notes
Rules for comparing 2 or more sinusoidal waveform or cosines waveform:
i) The expressions for the waveform must either be in sinus or cosines:
cos ωt = sin (ωt + (π/2)) @ sin ωt = cos (ωt – (π/2)).
ii) Both amplitudes must be positive or negative.
-sin ωt = sin (ωt ± π) @ -cos ωt = cos (ωt ± π)
iii) The frequency (f) or angular velocity (w) must be the same for all the waveforms.
Example 1.11 :
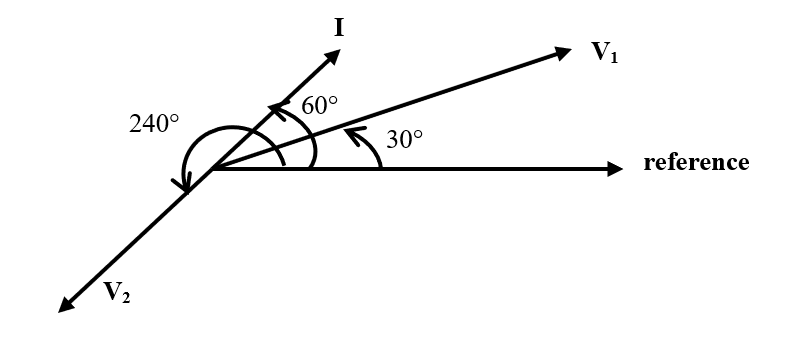
Determine the phasors representation for current and voltage waveform stated in (a) – (c). Draw the phasors diagram representation for the three waveforms on one plane.
- v1(t) =160 sin(314t + 30°)V
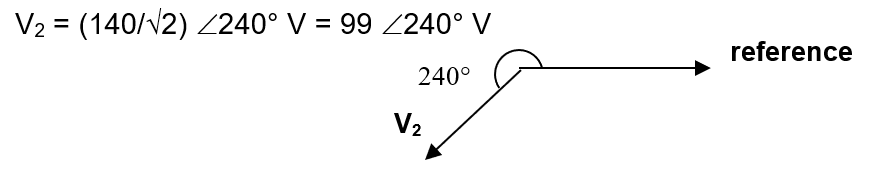
- v2(t) = -140 sin(314t + 60°) V
- i(t) = 60 cos(314t – 30°) A
Solution :
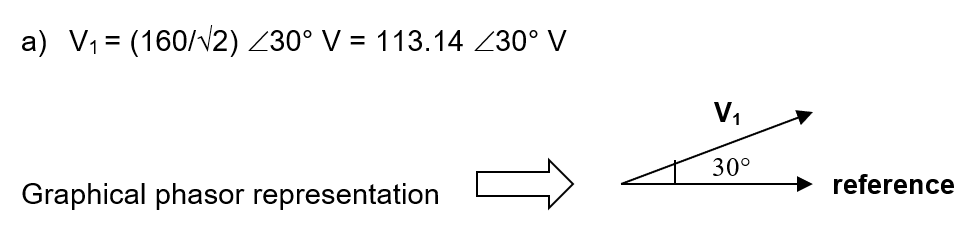
b) v2(t) = -140 sin(314t + 60°) V → v2(t) = 140 sin(314t + 60° + 180°) V
= 140 sin(314t + 240°) V
c) i(t) = 60cos(314t – 30°) A → i(t) = 60 sin(314t – 30° + 90°) A
= 60 sin(314t + 60°) A
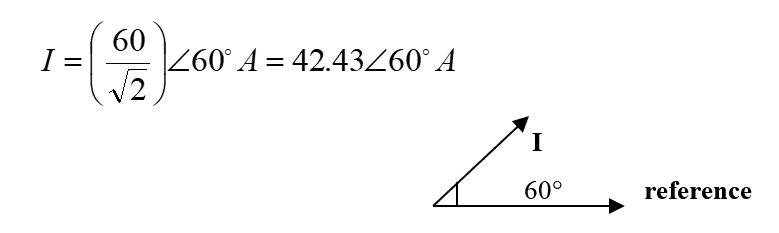
Phasors diagram representation for the three waveforms on one plane.
1.8 ANALYSIS OF AC CIRCUITS
When a time-varying ac voltage such as sinusoidal voltage is applied to a circuit, the circuit laws such as Ohm’s law, Kirchhoff’s laws, and the power formulas apply to ac circuits in the same way applied to dc circuits.
1.8.1 OHM’S LAW
Ohm’s law states that the voltage v across a resistor is directly proportional to the current i flowing through the resistor.
That is,
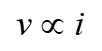
Equation 1.25
Ohm defined the constant of proportionality for a resistor to be the resistance, R. (The resistance is a material property which can change if internal or external conditions of the element are changed, e.g., if there are changes in temperature.) Thus, equation (1.25) becomes
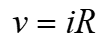
Equation 1.26
which is the mathematical form of Ohm’s law. R in equation 1.26 is measured in the unit of ohms, designated Ω. Thus, the resistance R of an element denotes its ability to resist the flow of electric current. So from equation 1.26 it can be deduced that
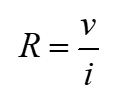
Equation 1.27
Power in resistive ac circuits is determined the same as for dc circuits except that values of current and voltage must be in rms value. The general power formulas for a resistive ac circuit as
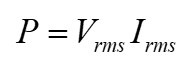
Equation 1.28
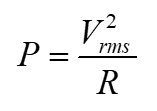
Equation 1.29
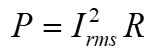
Equation 1.30
Example 1.12 :
An electric iron draws 2 A at 120 V. Find its resistance
Solution :
From Ohm’s law,
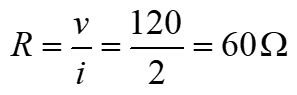
Related problem :
The essential component of a toaster is an electrical element (a resistor) that converts electrical energy to heat energy. How much current is drawn by a toaster with a resistor 24 Ω at 240 V?
Example 1.13 :
Determine the rms voltage across each resistor and the rms current in Figure 1.27. Calculate the total power supply to both resistors.
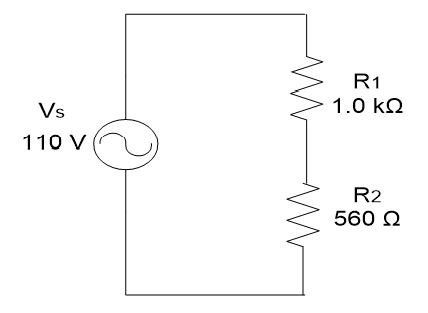
Figure 1.27
Solution :
The total resistance of the circuit is
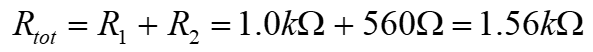
Use Ohm’s law to calculate the current
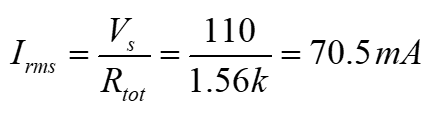
The rms voltage drop across each resistor is
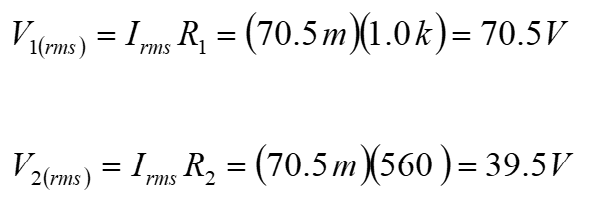
The total power is
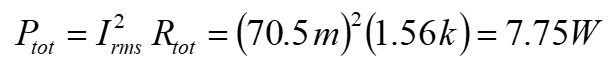
1.8.2 KIRCHHOFF’S LAW
Kirchhoff’s first law is based on the law of conservation of charge, which requires the algebraic sum of charges within a system cannot change.
Kirchhoff’s current law (KCL) states that the algebraic sum of current entering a node (or a closed boundary) is zero or the sum of currents entering a node is equal to the sum of currents leaving the node.
Mathematically, KCL implies that
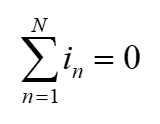
Equation 1.31
where N is the number of branches connected to the node and in is the nth current entering or leaving the node. By this law, current entering a node may be regarded as positive, while current leaving the node may be taken as negative or vice versa.
Example 1.14 :
From figure 1.28, proof that
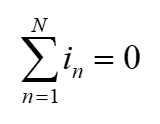
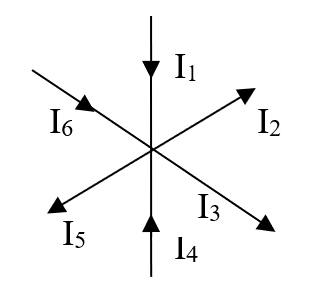
Figure 1.28: Currents at a node illustrating KCL
Solution :
By applying KCL at node A,
I1 – I2 – I3 + I4 – I5 + I6 = 0 or I1 + I4 + I6 = I2 + I3 + I5
Kirchhoff’s second law is based on the principle of conservation of energy.
Kirchhoff’s voltage law (KVL) states that the algebraic sum of all voltages around a closed loop (or path) is zero or the sum of voltage drops is equal to the sum of voltage rises.
Mathematically, KVL implies that
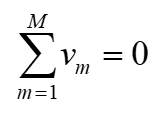
Equation 1.32
where M is the number of voltages in the loop and vm is the mth voltage. To illustrate the KVL, consider the circuit in Figure 1.29.
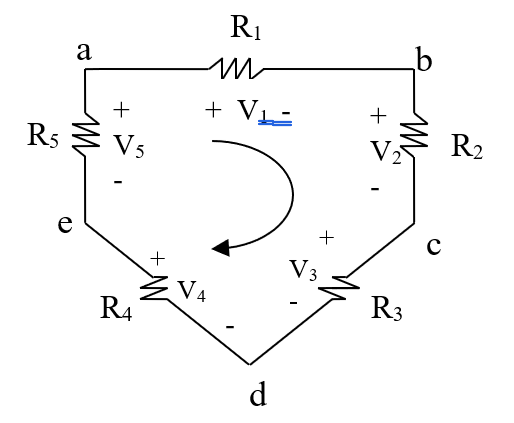
Figure 1.29: A single-loop circuit illustrating KVL
The sign on each voltage is the polarity of the terminal encountered first as we travel around the loop. Suppose we go clockwise around the loop as shown in Figure 1.29; then voltages would be:
+ V1, + V2, +V3, -V4, -V5 = 0
Rearranging terms gives
V4 + V5 = +V1 + V2+ V3
Example 1.15 :
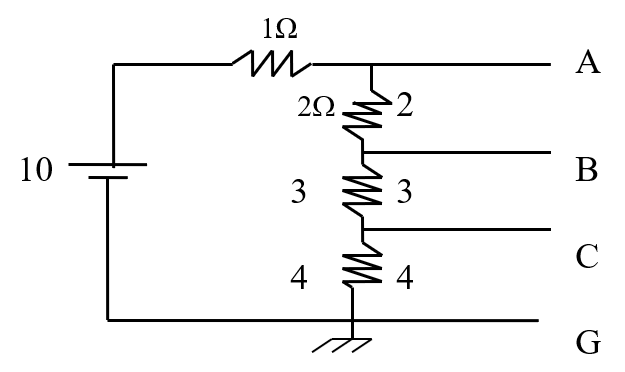
Figure 1.30
Refer Figure 1.30, determine VCG, VBC, VAB, VBG, VAC, VAG, VGC, VCB, VBA, VGB, VCA, VGA
Solution:
VCG = 4V VBC = 3V VAB = 2V
VBG = 7V VAC = 5V VAG = 9V
VGC = -4V VCB = -3V VBA = -2V
VGB = -7V VCA = -5V VGA = -9V
Related problem :
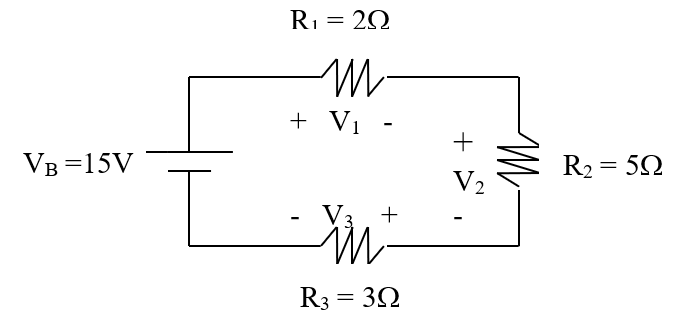
Figure 1.31
Refer to circuit in Figure 1.31,
- Find Rtotal
- Find current flow in the circuit
- Determine V1, V2 and V3
1.9 SUPERIMPOSED DC AND AC VOLTAGES
In many practical circuits, both ac and dc voltages are combined, for example is in amplifier circuits where ac signal voltages are superimposed on dc operating voltages.
Figure 1.32 shows a dc source and an ac source in series. These two voltages will add algebraically to produce an ac voltage “riding” on a dc level, as measured across the resistor.
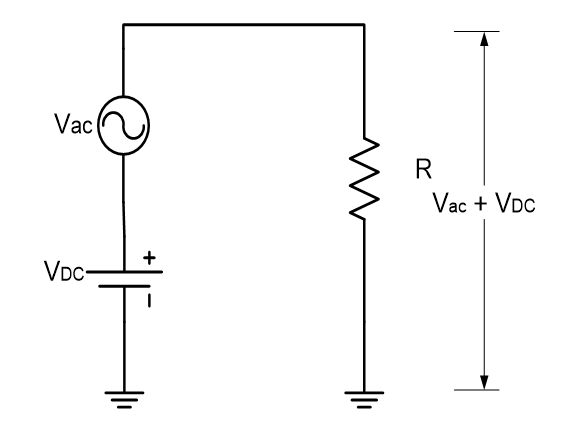
Figure 1.32: Superimposed ac and dc voltages
If VDC is greater than the peak value of the sinusoidal voltage, the combined voltage is a sine wave that never reverses its polarity and is therefore non-alternating. That is the sine wave is riding on the dc level, as shown in Figure 1.33 (a). If VDC is less than the peak value of the sine wave, the sine wave will be negative during a portion of its lower half-cycle, as shown in Figure1.33 (b), and is therefore alternating. In either case, the sine wave will reach a maximum voltage equal to VDC + Vp and it will reach a minimum voltage equal to VDC – Vp.
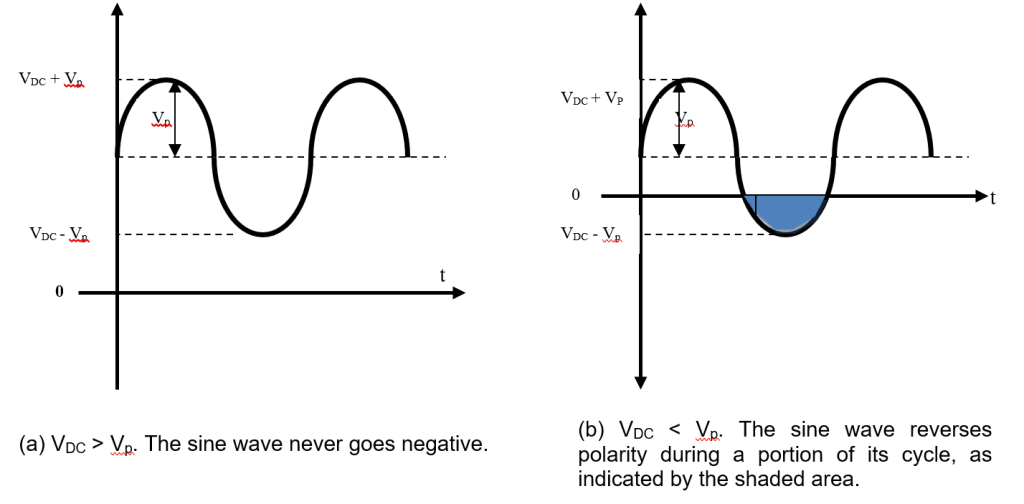
Figure 1.33: Sine waves with dc levels
Example 1.16:
Determine the maximum and minimum voltage across the resistor in each circuit of Figure 1.34 (a) and (b)

Solution :
In Figure 1.34 (a), the maximum voltage across R is
Vmax = VDC + Vp = 12 V + 10 V = 22 V
The minimum voltage across R is
Vmin = VDC – VP = 12 V – 10 V = 2 V
Therefore, VR(tot) is a non-alternating sine wave that varies from +22 V to +2V.
In Figure 1.34 (b), the maximum voltage across R is
Vmax = VDC + Vp = 6 V + 10 V = 16 V
The minimum voltage across R is
Vmin = VDC – Vp = 6 V – 10 V = -4 V
Therefore, VR(tot) is an alternating sine wave that varies from +16 V to – 4 V.
1.10 SUMMARY
- The sine wave is a time varying, periodic waveform.
- Alternating current changes direction in response to changes in the polarity of the source voltage.
- One cycle of an alternating sine wave consists of a positive alternation and negative alternation.
- Two common sources of sine waves are the electromagnetic ac generator and the electronic oscillator circuit.
- A full cycle of a sine wave is 360°, or 2π radians. A half-cycle is 180°, or π radian. A quarter-cycle is 90°, or π/2 radian.
- A sinusoidal voltage can be generated by a conductor rotating in a magnetic field.
- Phase angle is the difference in degrees or radians between a given sine wave and a reference sine wave.
- The angular position of a phasor represents the angle of the sine wave with respect to 0° reference, and the length or magnitude of a phasor represents the amplitude.
- Conversion of sine wave values are summarized in Table 1.0.
| To change from | To | Multiply By |
| Peak | rms | 0.707 |
| Peak | Peak-to-peak | 2 |
| Peak | Average | 0.637 |
| rms | Peak | 1.414 |
| Peak-to-peak | Peak | 0.5 |
| Average | Peak | 1.57 |
10. Ohm’s law states that the voltage v across a resistor is directly proportional to the current i flowing through the resistor.
That is,
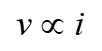
Ohm defined the constant of proportionality for a resistor to be the resistance, R.
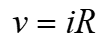
- Kirchhoff’s current law (KCL) states that the algebraic sum of current entering a node (or a closed boundary) is zero or the sum of currents entering a node is equal to the- sum of currents leaving the node. Mathematically, KCL implies that
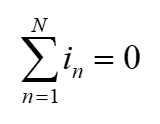
where N is the number of branches connected to the node and in is the nth current entering or leaving the node.
12. Kirchhoff’s voltage law (KVL) states that the algebraic sum of all voltages around a closed loop (or path) is zero or the sum of voltage drops is equal to the sum of voltage rises. Mathematically, KVL implies that
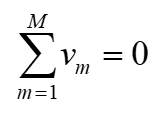
where M is the number of voltages in the loop and vm is the mth voltage.
1.11 SELF-ASSESSMENTS
1.What is the general equation for sinusoidal waveform?
2. A sinusoidal voltage with a maximum amplitude of 150 V and an amplitude of 15 V at t = 0 second. Determine the voltage expression n(t) for one complete cycle taken in 1 ms. second. Sketch the waveform.
3. Given the sinusoid 5 sin(4πt – 60°), calculate its amplitude, phase, angular frequency, period, and frequency.
4. Given n(t) = 8 cos (8t + 40°)V
i) Calculate the period, T
ii) State the phase relation between the voltage and current i(t) = 6 cos (8t – 80°) A. Sketch both waveforms.
5. Given in time-domain,
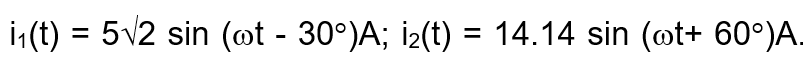
Determine i1(t) + i2(t).

