UNIT 3: RL CIRCUITS
INDEX
| 3: RL CIRCUITS |
| 3.1 Sinusoidal Response of RL Circuits 3.2 Impedance and Phase Angle of Series RL Circuits 3.3 Analysis of Series RL Circuits 3.3.1 Ohm’s Law 3.3.2 Phase Relationships of the Current and Voltages 3.4 Impedance and Phase Angle of Parallel RL Circuits 3.4.1 Conductance, Susceptance and Admittance 3.5 Analysis of Parallel RL Circuits 3.5.1 Phase Relationships of the Current and Voltages 3.6 Combination of Series and Parallel RL Circuits 3.7 Power in RL Circuits 3.7.1 The Power Triangle for RL Circuits 3.7.2 Power Factor 3.7.3 Power Factor Correction 3.8 Summary 3.9 Self-Assessments |
Learning Objective:
The objective of this unit is to:
- Determine the impedance and phase angle of series, parallel and combination series-parallel RL circuits.
- Apply Ohm’s law and basic mathematic in analyzing the RL circuits.
- Draw phasor diagram for RL circuits
- Determine the conductance, susceptance and admittance for RL circuits.
- Determine power and power factor in RL circuits.
- Introduce to power factor correction.
Learning Outcome:
At the end of lesson student should be able:
- Familiarize with the terms of impedance, conductance, susceptance and admittance of RL circuits.
- Determine the phase relationship between current and voltage of RL circuit.
- Analyze simple RL circuits using basic circuit law.
- Determine power and power factor in RL circuits.
3.1 SINUSOIDAL RESPONSE OF RL CIRCUITS
When a sinusoidal voltage is applied to a circuit consisting of resistor, R connected in series or parallel with inductor, L, the current flowing through the circuit, I and the voltages across the resistor and inductor, VR and VL respectively are also in a form of sinusoidal and have the same frequency as the source voltage. The inductance causes a phase shift between the voltage and the current that depends on the relative values of the resistance and the inductive reactance.
3.2 IMPEDANCE AND PHASE ANGLE OF SERIES RL CIRCUITS
Figure 3.0(a) shows the basic series RL circuit. To analyze the circuit, the inductor L is converted in terms of reactance, XL while the other element remains the same as shown in Figure 3.0(b).
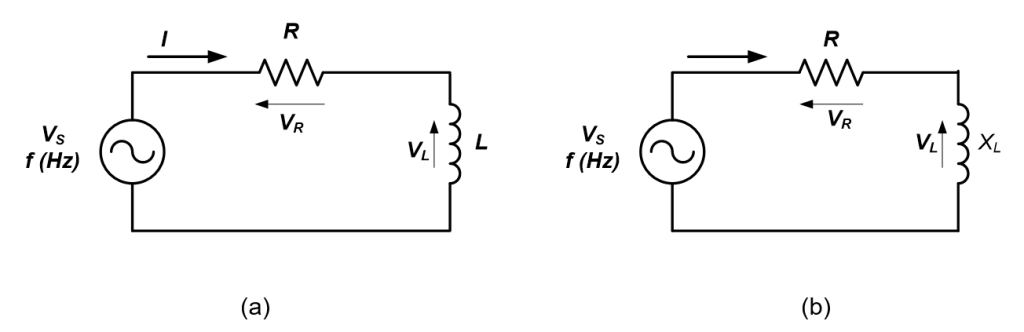
The impedance of a series RL circuit consists of resistance and inductive reactance. The symbol of impedance and inductive reactance are Z and XL respectively. Both units are ohm.
Thus the inductive reactance is:
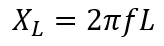
The impedance of the circuit is:
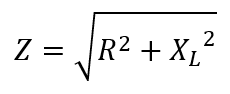
A phasor representation of the resistance R, inductive reactance, XL and the impedance is shown in Figure 3.1(a) Figure 3.1(b) is obtained after repositioning the phasors and is called the impedance triangle. The length of each phasor represents the magnitude of the quantity, and q is the phase angle of the impedance.
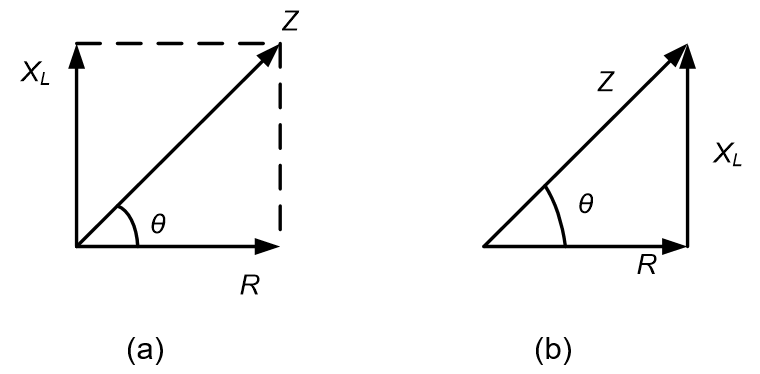
The phase angle, θ, is expressed as
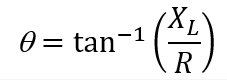
Example 3.1:
Find the impedance and phase angle of circuit in Figure E3.1(a) and Figure E3.1(b).
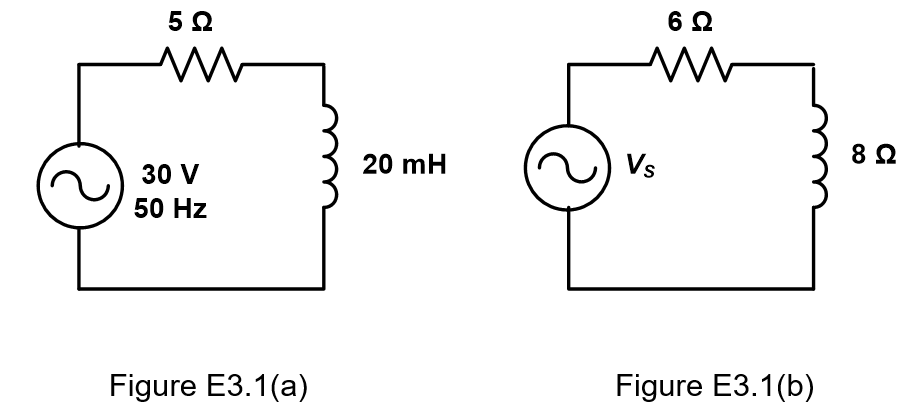
Solution:
Figure E3.1(a) (a); The inductor reactance,
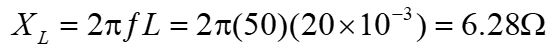
The impedance is:
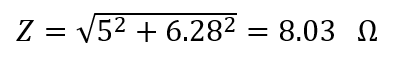
The phase angle of the circuit is

Figure E3.1(b):
The impedance:
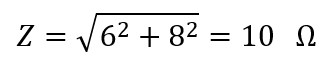
The phase angle:
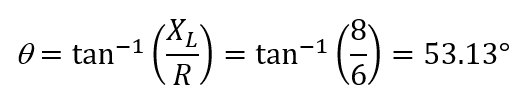
3.3 ANALYSIS OF SERIES RL CIRCUITS
In analyzing a series RL circuit, Ohm’s Law and Kirchhoff’s voltage law will be used. The phase relationships between the voltages and the current are also can be determined.
3.3.1 OHM’S LAW
The application of Ohm’s law to series RL circuits involves the use of the quantities of Z, V and I. The three equivalent forms of Ohm’s law are as follows:
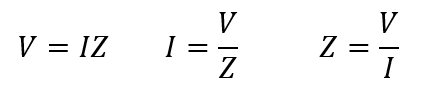
3.3.2 PHASE RELATIONSHIPS OF THE CURRENT AND VOLTAGES
Referring to Figure 3.0(b), the current flowing through the circuit, I is the same through both the resistor and the inductor. Therefore,
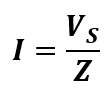
Thus the voltages across resistance, VR, and inductive reactance, VL are:
VR = IR
VL = IXL
The resistor and inductor voltage are also can be obtained using voltage division as follows:
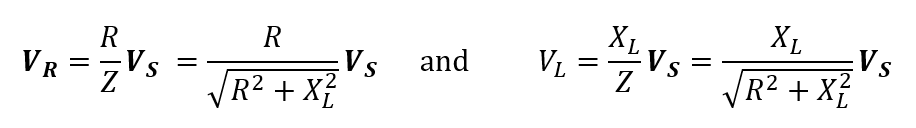
In series RL circuit, the voltage source, VS must equal to the sum of voltage drops in resistor and inductor. However, the magnitude of VS is not simply equal to the sum of magnitude VR and VL since they are not in phase with each other. Therefore, VS is the phasor sum of VR and VL and can be expressed as
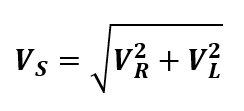
In order to draw a phasor diagram for series RL circuit, there a
(i) The current flowing through resistor is in phase with the voltage across it.
(ii) The current flowing through inductor lags voltage across it by 90°.
Thus, by taking the current as a reference (because all the currents are equal), the phasor diagram for all voltages and current of a series RL circuit can be illustrated in Figure 3.2,
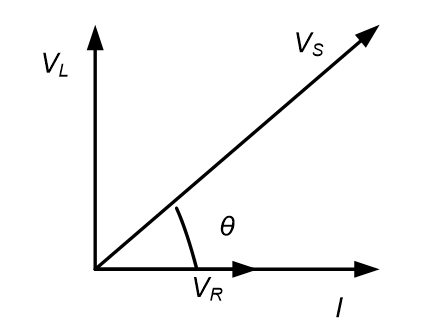
From Figure 3.2, it can be observed that
(i) The current, I, flowing through the circuit is in phase with voltage across resistance, VR.
(ii) The current, I, lags the supply voltage, VS by θ°.
(iii) The current I lags the inductor voltage, VL by 90°.
The waveform diagram for current and all voltages is shown in Figure 3.3
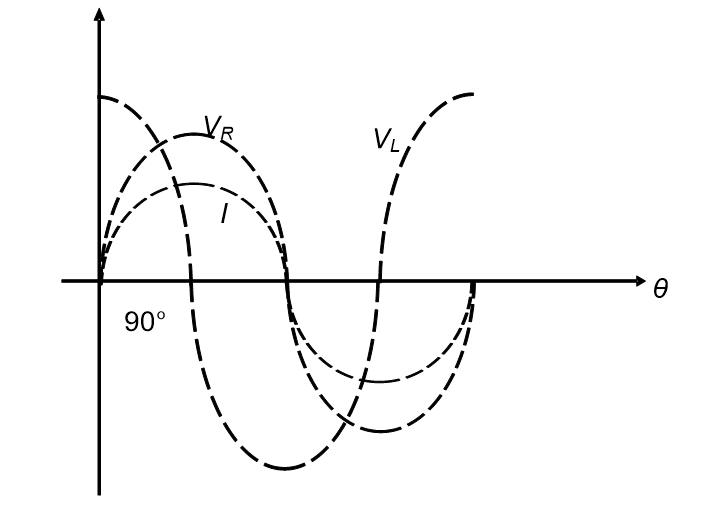
Example 3.2:
Refer to Figure E3.2
(i) Determine the total impedance
(ii) Calculate the current, I
(iii) Determine the resistor and inductor voltages.
(iv) Draw a phasor diagram showing all the voltages and current in the circuit.
(v) Write the relationship between the source current and the source voltage.
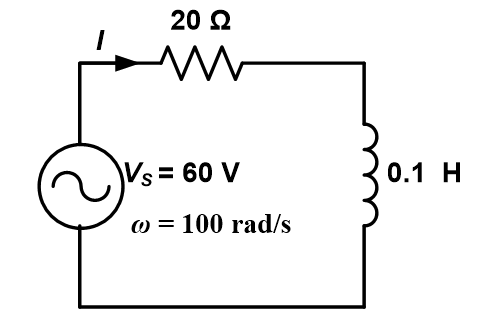
Solution:
The reactance,
XL = jωL = j(100)(0.1) = j10 Ω
(i) The total impedance can be obtained as follow:
The magnitude of total impedance;
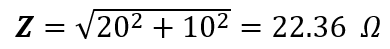
And the phase angle of total impedance is:
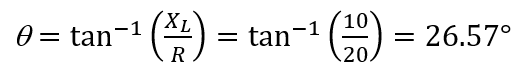
Therefore,
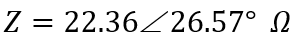
(ii) The current, I :
From ohm’s law,
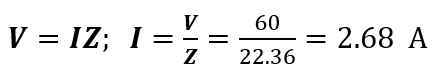
(iii) The resistor voltage,
VR = IR = 2.68 x 20 = 53.6 V
The inductor voltage,
VL = IXL = 2.68 x 10 = 26.8 V
The voltage division can also be used to determine the voltage across resistor and inductor, i.e.,
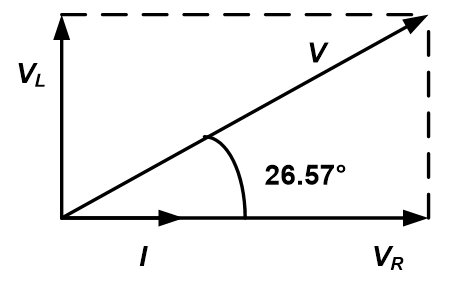
(iv) Phasor diagram:
Take current as a reference, as the current flowing through R and L are equal.
For resistor : The voltage across resistor is in phase with the current flowing through
it.
For inductor : The voltage across inductor leads current flowing through it by 90°.
The current I lags the source voltage by 26.57°.
Therefore, the phasor diagram is as shown below.
Checking: The source voltage,
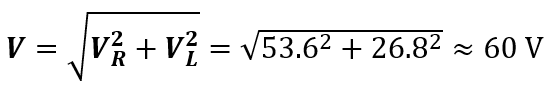
equal as given in the question.
(v) The current I lags the source voltage by 26.57° or the source voltage leads the current I by 26.57°.
3.4 IMPEDANCE AND PHASE ANGLE OF PARALLEL RL CIRCUITS
Figure 3.4(a) shows the basic parallel RL circuit. To analyze the circuit, the inductor L is converted in terms of reactance, XL while the other element remains the same as shown in Figure 3.4(b).
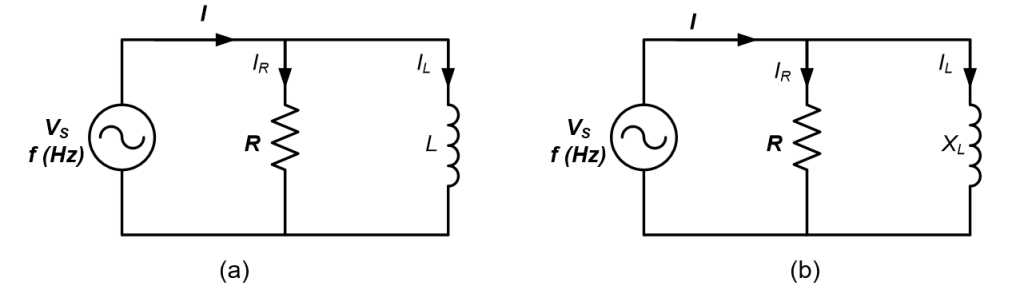
The impedance in magnitude and phase angle can be obtained as follows:
The impedance of the circuit:
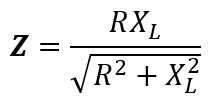
And the phase angle is
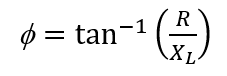
3.4.1 CONDUCTANCE, SUSCEPTANCE AND ADMITTANCE
Conductance, G is :
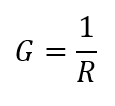
Susceptance, B :
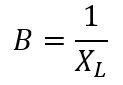
Admittance, Y :
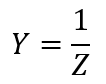
The unit for G, B and Y is the Siemens (S)
In the basic parallel RL circuit shown in Figure 3.4(b), the admittance and phase angle of admittance are given by:
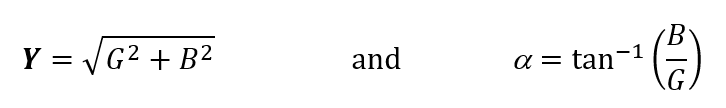
Example 3.3:
Determine the total admittance and total impedance for the circuit in Figure E3.3
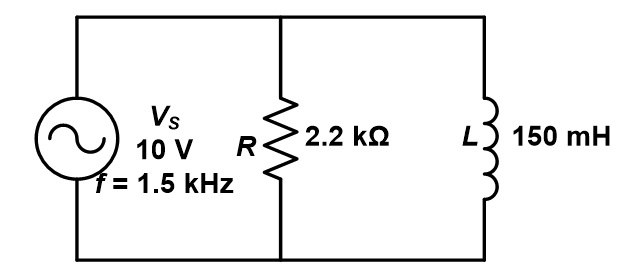
Solution:
The conductance,
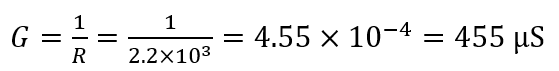
The susceptance;
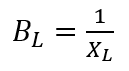
Where
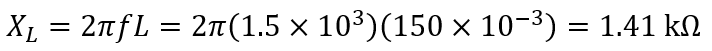
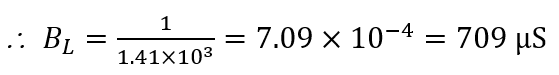
Thus, the admittance is:
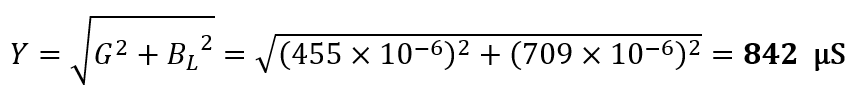
The total impedance,

3.5 ANALYSIS OF PARALLEL RL CIRCUITS
Ohm’s and Kirchhoff’s current law are used to analyze parallel RL circuit.
3.5.1 PHASE RELATIONSHIPS OF THE CURRENTS AND VOLTAGES
From Figure 3.4(b), as we can see, the voltage across resistor and the voltage across inductor are equal to the source voltage. All the voltages are in phase and of same magnitude.
VS = VR = VL
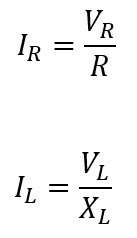
By using ohm’s law, the current flowing through resistor, IR and inductor, IL can be written as:
If the value of the supplied current, I is known, the IR and IL can be obtained using current division as
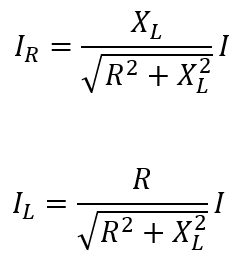
The current, IR is in phase with VR and the current ILlags VL by 90°. Thus by taking voltage as a reference, the phasor diagram for voltage and current of series RL parallel is illustrated in Figure 3.5.
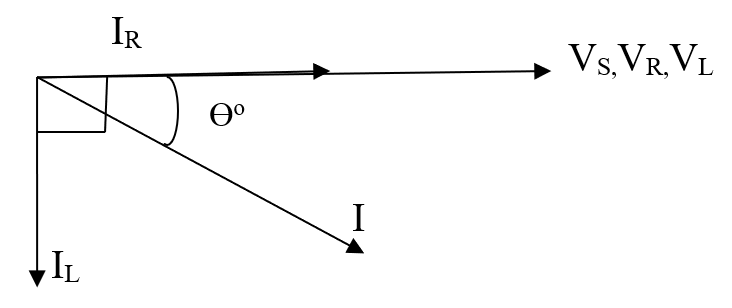
From Figure 3.4 (b), by using Kirchhoff’s law, the total current I, must equal to the sum of current IR and IL. However, the IR and ILare not in phase as shown in Figure 3.5. Thus, the total current, I is the phasor sum of the two branch currents and is expressed as:
From Figure 3.5, it can be observed that,
(i) Current IR is in phase with voltage VS (VS = VL = VR)
(ii) Current IL is lagging VS by 90°
(iii) Current I lags VS by ϴ°.
Example 3.4:
Refer to Figure E3.4.
(i) Determine the resistor current, the inductor current and the total current.
(ii) Determine the phase angle of the circuit.
(iii) Draw the phasor diagram for voltage and currents.
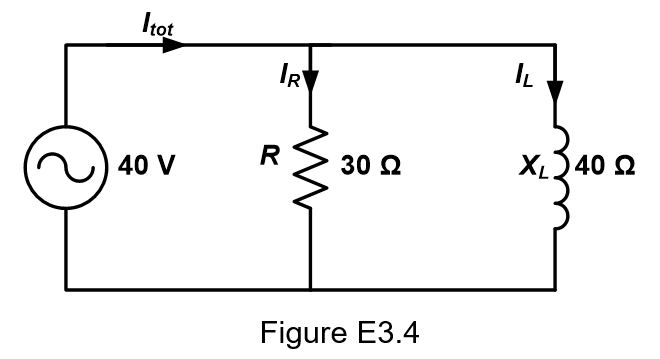
Solution:
(i) The resistor current,

The inductor current,
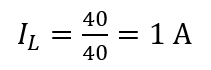
the total current,

(ii) The phase angle of the circuit is:
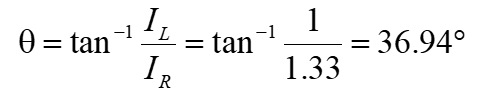
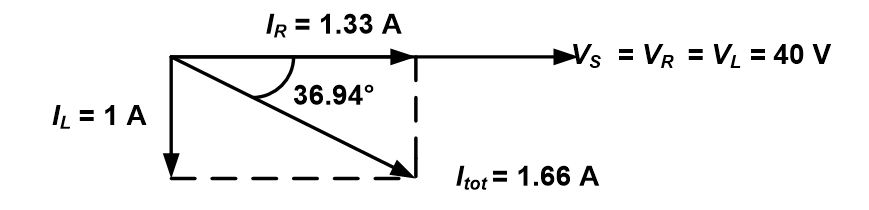
(iii) Phasor diagram,
Take voltage as a reference because source voltage, resistor voltage and inductor voltage are equal in magnitude and in phase. Then we know that,
(a) the current IR, is in phase with the source voltage (since source voltage is equal to voltage across resistor
(b) The current IL, lags source voltage by 90°.
Thus, the phasor diagram is illustrated as below:
3.6 COMBINATION OF SERIES AND PARALLEL RL CIRCUITS
In this section, the same concepts studied in the previous sections are used to analyze circuits. The following two examples illustrate the procedure used to analyze a series-parallel reactive circuit.
Example 3.5:
In the series-parallel RL circuit of Figure E3.5, determine the values of the following:
(a) Ztot (b) Itot (c) ϴ
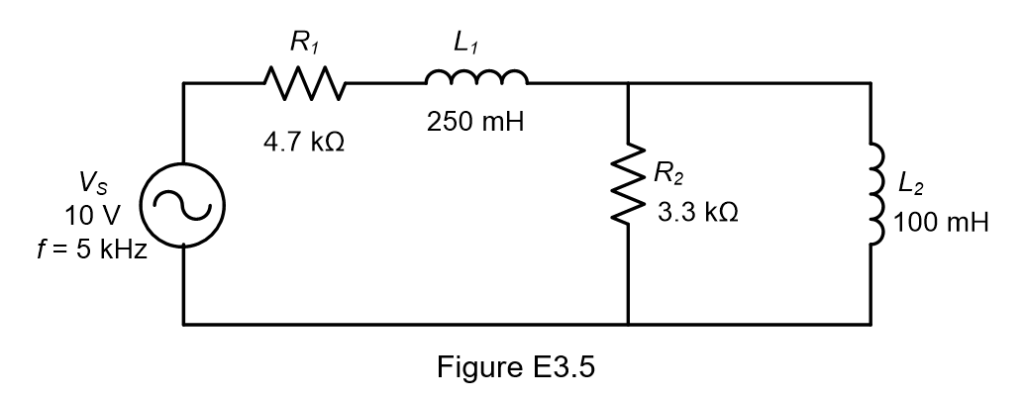
Solution:
(a) The magnitude of the inductive reactances are:
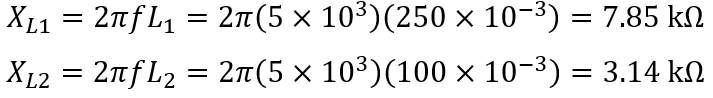
The Figure E3.5 can be redrawn as shown in Figure E3.5(a) where Req and Xeq are the series equivalent values for the parallel portion (R2 and X2).
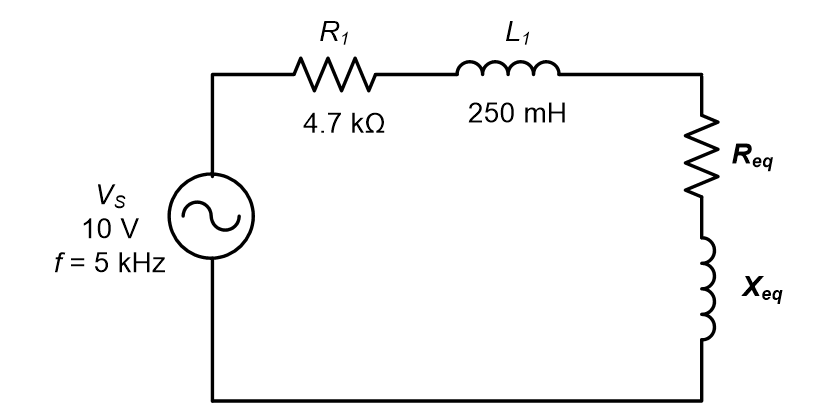
The total resistance is given by:
Rtot = R1 + Req
The total reactance is:
Xtot = X1 + Xeq
Thus, total impedance is:
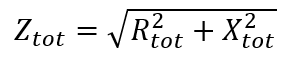
Therefore, the first thing that we have to do is to calculate the value of Req and Qeq.
Determination of the impedance for parallel portion (z2):
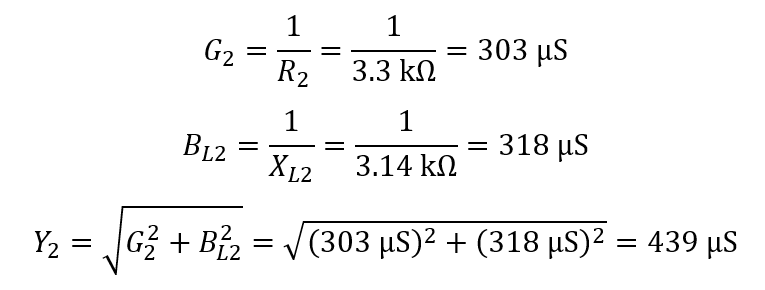
Then
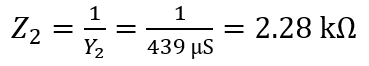
The phase angle is
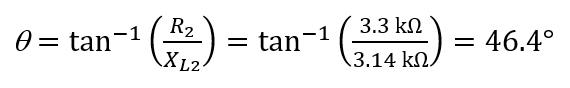
Thus the impedance triangle for Z2 is:
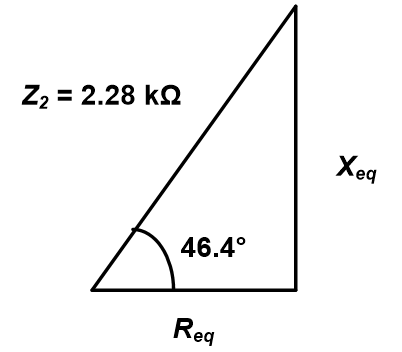
From the impedance triangle, the value of Req and Xeq can be determined:
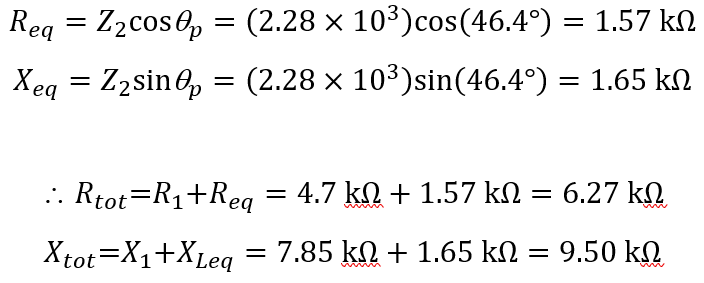
Therefore, total impedance of the circuit is:

(b) From Ohm’s law,
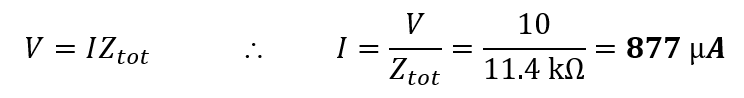
(c) From Figure E3.5(a), the phase angle is:
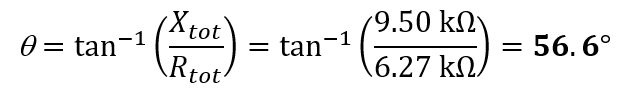
Since the total equivalent circuit consists of resistor series with inductor, the current Itot lags VS by 56.6°.
Example 3.6:
Determine the voltage across each component in Figure E3.6. Draw phasor diagram.
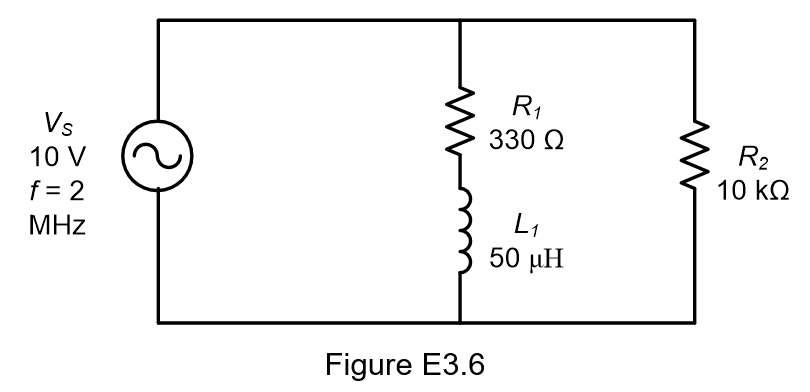
Solution:
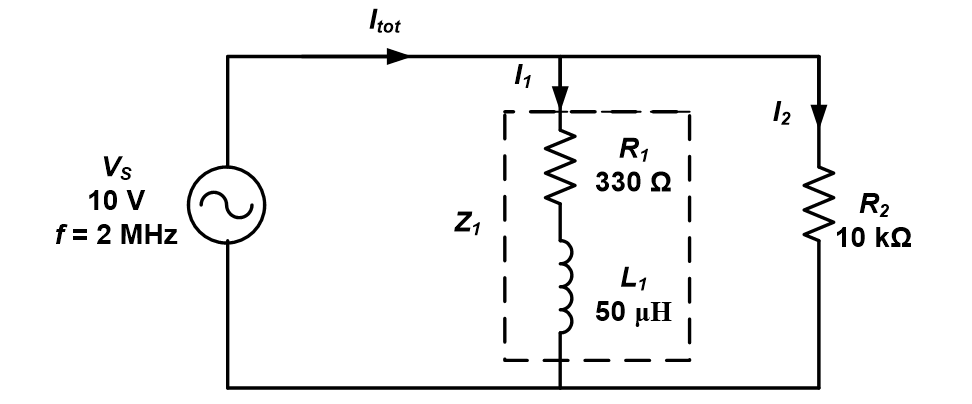
First, calculate XL1.
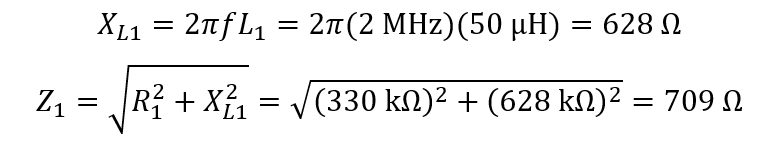
The branch currents, I1 and I2 are:
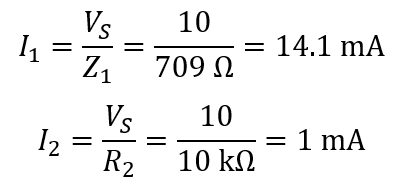
The voltage drops of each element.
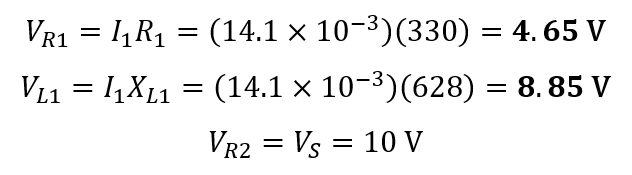
The phase angle of Z1 :
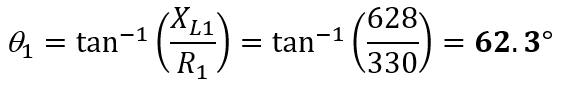
The phase angle of R2 is 0°, since VS is in phase with I2.
To draw a phasor diagram, determine the phase relationship between currents and voltages of the circuits as follow.
i) take VS as reference. Since VR2 is equal to VS both in magnitude and angle, VR2 is in phase with VS.
ii) I1 lags VS by 62.3°
iii) VR1 is in phase with IR1.
iv) I1 lags VXL1 by 90°.
The phasor diagram for Figure E3.6 is shown below.

3.7 POWER IN RL CIRCUITS
In purely resistive ac circuit, all of the energy delivered by the source is dissipated in the form of heat by the resistance. In a purely inductive ac circuit, all of the energy delivered by the source is stored by the inductor in its magnetic field during a portion of the voltage cycle and then returned to the source during another portion of the cycle so that there is no net energy conversion to heat. When there is both resistance and inductance, some of the energy is alternately stored and returned by the inductance and some is dissipated by the resistance. The amount of energy converted to heat determined by the relative values of the resistance and the inductive reactance.
When the resistance in a series RL circuit is greater than the inductive reactance, more of the total energy delivered by the source is dissipated by the resistance than is stored and returned by the inductor. When the reactance is greater than the resistance, more of the total energy is stored and returned than is converted to heat.
The power dissipated in a resistor is called real power or active power or true power and the power in an inductor is called reactive power. The unit of active power is the watt (W) and the unit of reactive power is the VAR (volt-ampere-reactive).
Active power, Pactive = I2R =V2/R (3-20)
Reactive power, QL = I2XL = V2/XL (3-21)
3.7.1 THE POWER TRIANGLE FOR RL CIRCUITS
The impedance triangle for series RL circuit is shown in Figure 3.1(b) and shown again in Figure 3.6(a). By multiplying R, XL and Z with I2, its gives I2R, I2XL and I2Z respectively as shown in Figure 3.6(b). Therefore the power triangle for RL circuit is shown in Figure 3.6(c).
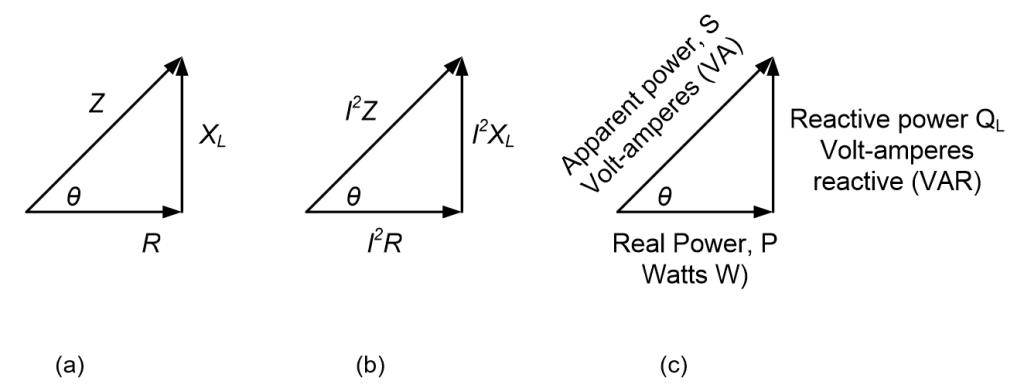
The resultant power I2Z represents the apparent power, S. At any instant in time, S is a total power that appears to be transferred between the source and the RL circuit. Part of the apparent power is real power and part of it is reactive power. The unit of apparent power is volt-ampere (VA). The expression for apparent power is
S = I2Z = VI (3-22)
From Figure 3.6(c), it is be observed that,
P = S cosϴ = VIcosϴ (3-23)
QL = S sinϴ = VIsinϴ (3-24)
Where, V and I are the source voltage and current respectively.
If Z = R (purely resistive),ϴ = 0°. Therefore P = VI watt and QL = 0 VAR
If Z = XL (purely inductive),ϴ = 90°, so P = 0 watt. It is shown that there is no power dissipated in an ideal inductor.
3.7.2 POWER FACTOR
The power factor is equals the cosine of ϴ (PF = cos ϴ). As the phase angle between the source voltage and the total current increases, the power factor decreases, indicating an increasingly reactive circuit. A smaller power factor indicates less real power and more reactive power. The power factor of inductive loads is called a lagging power factor because the current lags the voltage.
The power factor is very important in determining how much useful power (real power) is transferred to a load. The highest power factor is 1, which indicates that all of the current to a load is in phase with the voltage. At this condition, the circuit is purely resistive. When power factor is 0, all of the current to a load is 90° out of phase with the voltage. This case referred to purely inductive load.
Many practical loads are of inductive load, having power factor less than 1. Generally, a higher value of power factor i.e. 0.85 to 1 is desirable to ensure that more power can be delivered to the load.
Example 3.7:
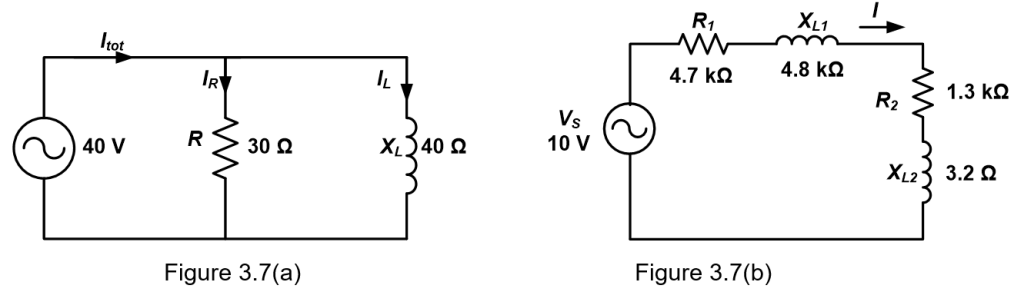
Determine the power factor, the active power, the reactive power and the apparent power for Figure E3.7 (a) and Figure 3.7 (b)
Solution:
(a) Figure 3.7(a)
True power is the power that dissipated in R, PR :
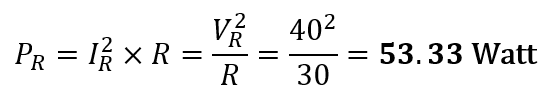
Reactive power, QL :
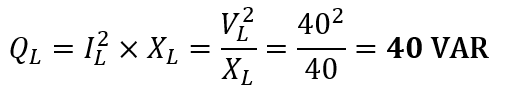
The power triangle is:
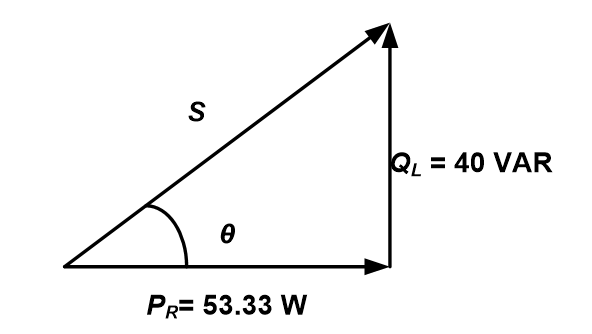
Therefore, the apparent power, S :
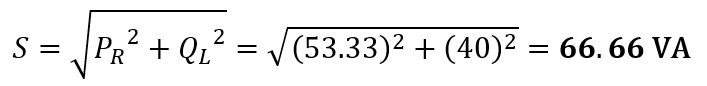
The phase angle is
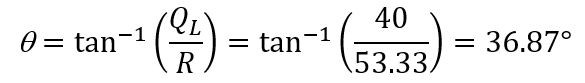
Thus the power factor is
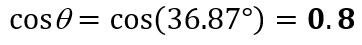
Figure 3.7(b)
The total resistance, Rtot and the total reactance XLtot are:

The total impedance is:
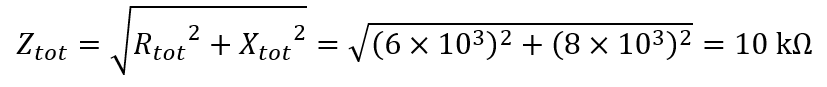
The current is:
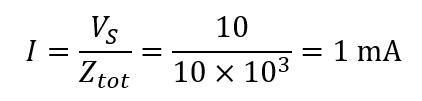
The phase angle is

Therefore, the power factor is
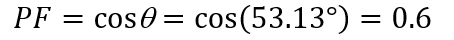
The true power is
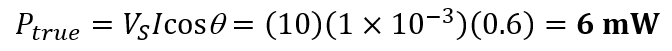
The reactive power is
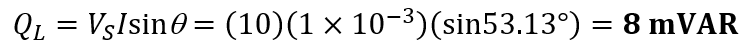
The apparent power is
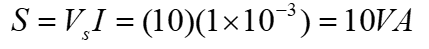
3.7.3 POWER FACTOR CORRECTION
The power factor of a series inductive load can be increased by the addition of a capacitor in parallel, as shown in Figure 3.8.
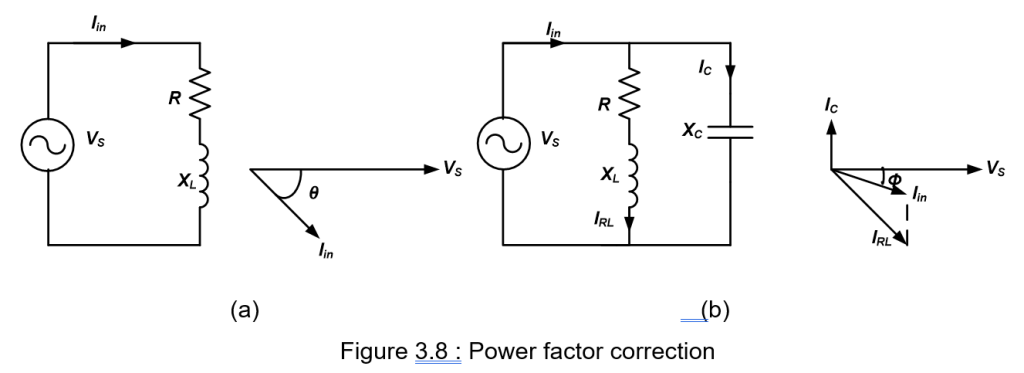
Figure 3.8 shows a typical inductive load consisting of reactance and inductance connected in series. Part (a) shows a load with power factor cos ϴ. The angle ϴ can be reduced to give high power factor. It can be done by placing a capacitor parallel with the inductive load as shown in part (b).
3.8 SUMMARY
1- When sinusoidal voltage is applied to an RL circuit, the current and all voltage drops are also sine waves.
2- Total currents in an RL circuit always lags the source voltage.
3- For resistance, the voltage across it is in phase with the current through it.
4- In inductor, the current lags the voltage by 90°.
5- The impedance of RL circuit is the ratio of source voltage to total current, i.e.
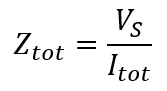
6- In an RL circuit, part of the power is resistive (real power) and part reactive (reactive power).
7- Power factor of an RL circuit is given by:
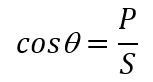
Where ϴ is the angle between the current and voltage of the circuit and can be calculated as:
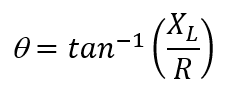
8- In an RL circuit, the power factor is said to be lagging.
9- Power factor of a series RL circuit can be increased by placing the capacitor across the series RL.
3.9 SELF-ASSESSMENTS
1- Determine the value of R and XL in a series RL circuit for the following values of impedance and phase angle.
(a) Z = 20 Ω, q = 45° (b) Z = 500Ω, q = 35°
(b) Z = 2.5 kΩ, q = 72.5° (c) Z = 998 Ω, q = 45°
2- A coil having a resistance of 10W and an inductance of 0.2H is connected to a 100 V, 50Hz supply. Calculate (a) the impedance of the coil, (b) the reactance of the coil, (c) the current taken and (d) the phase difference between the current and the voltage.
3- An impedance coil takes 480 W of power and 5 A from a 120-V, 50 Hz source. Calculate
a) Power factor of the circuit
b) The impedance, resistance and reactance of the coil and
c) Phase angle between current and voltage
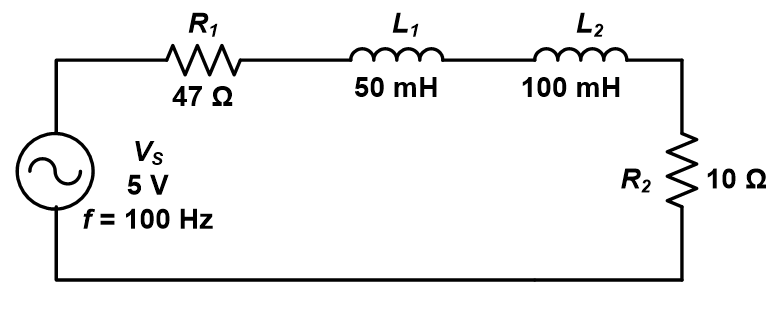
4- Determine the impedance, voltage across the total resistance and total inductance, phase angle, total real power, total reactive power and power factor of Figure below. Repeat the question if the frequency of the source is increased to 1 kHz.